「本番力を仕上げよう」 ~昭和薬科模試・開邦×球陽中模試~
ガゼットでは《本番力を仕上げよう》 をテーマに10月2日(日)に『第2回開邦中×球陽中模試』、10月9日(日)に『昭和薬科模試』を開催します。開邦・球陽中学、昭和薬科中学などを志望されている皆さんは、ぜひ挑戦してください。

企画戦略部 部長 太田 真光さん :広報担当 松田 麗香さん
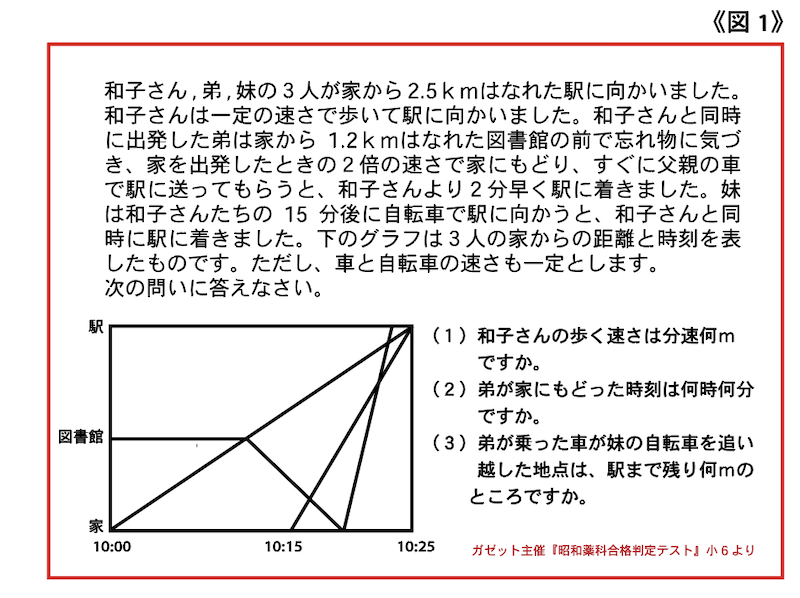
松田「さて今回の模試は、《本番力を仕上げよう!》がテーマとなっています。開邦中学の算数独自検査では、毎年グラフを絡めた問題が出題されており、2022年度の昭和薬科中学の算数でも速さとグラフの問題が出ていましたので、その問題(図1)の解き方等を通じて、《本番力》を意識するポイントを紹介していきます。」
松田「《本番力》を意識するポイントとはどんなことに気を付ければよいのでしょうか。」
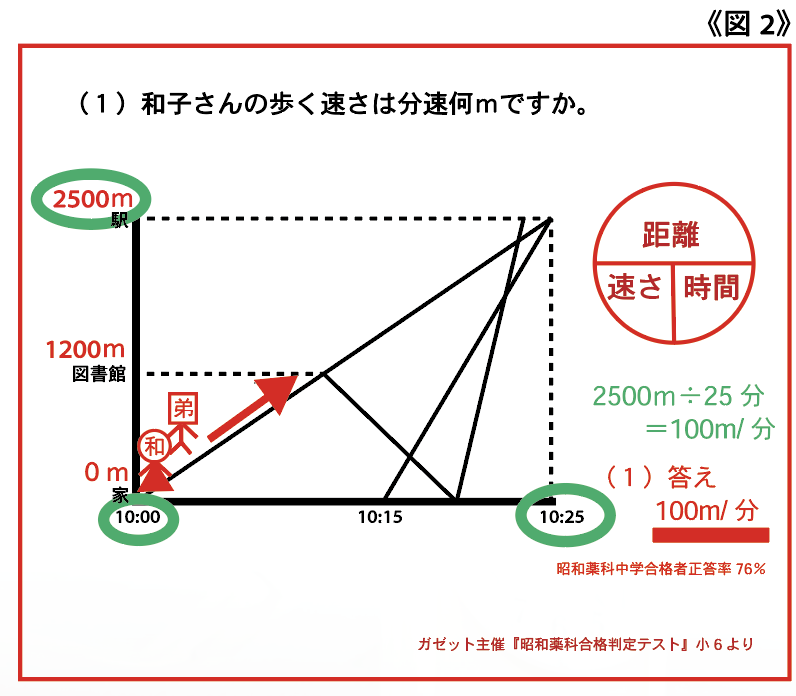
太田「いろいろありますが、グラフや表を利用した問題は、数値などのわかる情報を書き込んでいきます。そして、それら情報を踏まえて読み解いていきます。グラフの距離と時刻に着目すると、10時に出発した和子さんは25分後に2500mはなれた駅に到着することがわかります。すると和子さんの歩く速さは、2500m÷25分で、(1)の答えは毎分100mです。」(図2)
松田「なるほどグラフの中にヒントになる情報が隠されているわけですね。それを見つけていけば答えにたどりつけるのですね。」
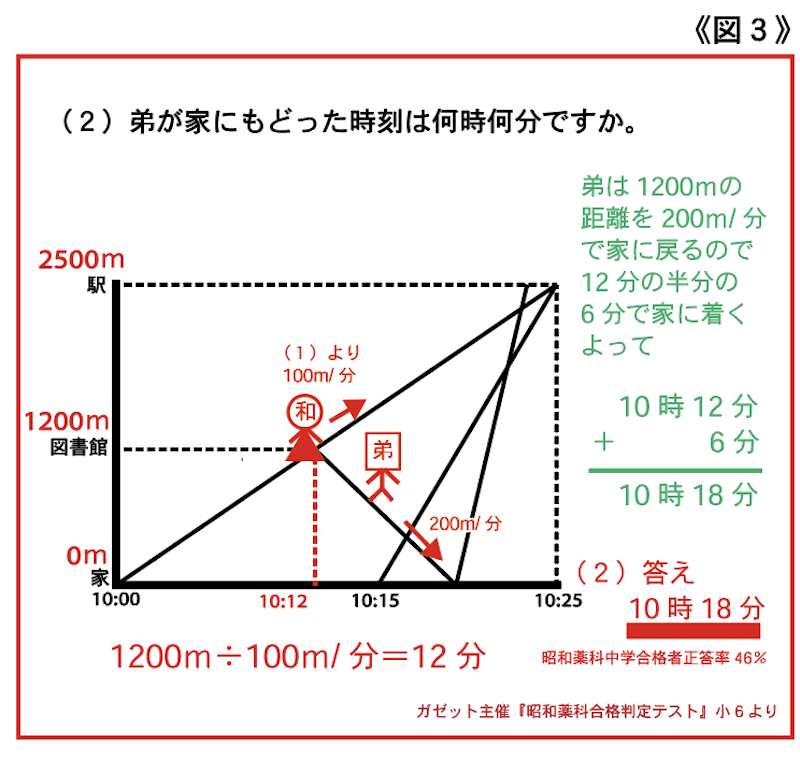
太田「その通りです。もちろんグラフに書いてある情報を読み解くために、速さの公式などは、当然知っておかなければなりません。さらに着目する部分を見極めることで次の道筋が見えてきます。(2)は省略しますが、答えは10時18分です。」(図3)
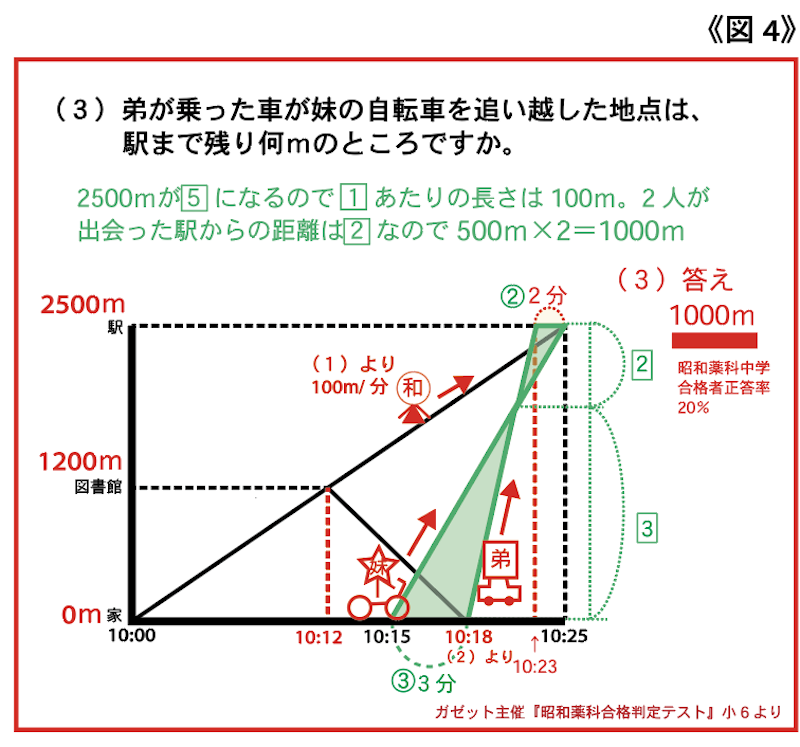
《本番力を仕上げよう》【ポイント①】 ・問題文に書いている条件や数値は必ず書き込む習慣がついているか確認しましょう! 太田「(3)は『旅人算』のやり方で解くのがオーソドックスですが『相似な図形』を利用したやり方で説明します。まず(2)より弟が家にもどった時刻は10時18分、父親の車に乗った弟が駅に着くのは、和子さんが到着する2分前ですから10時23分です。(図4)緑色で塗られた部分に着目すると大小2つの三角形があることがわかります。グラフの横軸に沿って辺が引かれていますから2つの三角形は相似です。すると底辺に当たる部分は、それぞれ2分と3分、つまり辺の比は2:3です。すると高さに当たる部分の比も2:3となります。家から駅までの距離の比の合計は2+3で5となりますから、家から駅までの距離である2500mが比の大きさでは5ということになります。ですから比1あたりの大きさは2500÷5で500mです。
《本番力を仕上げよう》【ポイント②】 ・さまざまな解き方にふれ、自分の解きやすい方法を確立させましょう。 ・旅人算でも相似な図形でも理解できるようにし、解き方の幅を広げましょう。 松田「問題が進むと、ヒントになる情報を見つけるのも苦労しますね。でもグラフに隠された情報を読み取って、それらを整理することが大切ですね。」 太田「その通りです。ガゼットの公開模試は、今回取り上げたポイントの実践はもちろん、総合力を判定する模試として県内最大規模で実施しています。加えて、公開模試を受けた方を対象にオンライン保護者セミナーも予定しています。模試の受験特典として進呈する資料を基にして、開邦・球陽中学での『志願理由書』の書き方や、入試での『問題構成』についてアドバイス致しますので、ご希望の方は、公開模試及びオンライン保護者セミナーにぜひご参加ください。
new3.png)
